Liquidity Trees
Table of contents
- Introduction
- Concentrated Liquidity Market Makers
- Networking AMMs
- Simple Tree (Include New Dimension)
- How Do Liquidity Trees Generate Revenue?
- Various Tree Types
- Simulation Results
Introduction
In this section, we introduce a novel DeFi primitive which we call Liquidity Trees. These systems serve as an extension to DEX Liquidity Pools (LPs) and address the problem of increasing LP capital efficiency in a trustless manner. For instance, let’s consider an LP with a market cap of $100,000 USD, where only 2-5% is seen in daily trading volume. Consequently, 95-98% of that capital remains stagnant on any given day and does not earn a return on trading fees. Liquidity Trees address this issue by taking liquidity in those pools and converting them into continuous rebasing index tokens (CRITs). Sub-markets are created out of these CRITs, thus addressing what we term the Stagnant Liquidity inefficiency problem. These sub-markets are called child LPs, and the base LP from which these sub-markets are created is called the parent. This relationship is repeatable, where new CRITs can be created from the liquidity in these child LPs to form new sub-markets, thus creating a second layer of new child markets. This repeatable structure of transitioning indexed capital between these DEXes is what we call a Liquidity Tree.
Concentrated Liquidity Market Makers
In May 2021, Uniswap launched V3 as an upgrade to address the lazy liquidity problem, thus introducing the concentrated liquidity market maker (CLMM) protocol. The main idea behind this upgrade was to concentrate the liquidity within the active trading band, which virtually deepens the order book to make more liquidity available for trading; see Fig 1 for more detail. This protocol was arguably the first to address market efficiency through the automated market makers (AMMs) liquidity frequency distribution.
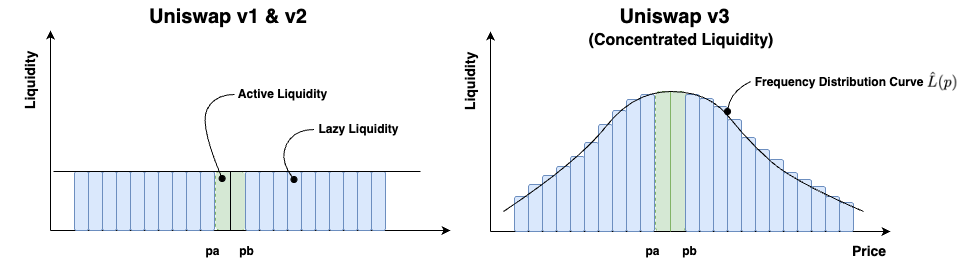
In our ETHDenver talk, we began discussing how the inactive capital within Uniswap V2, known as Lazy Liquidity, which sits outside the active trading range, does not earn yield. This is what’s known as poor capital efficiency. Uniswap V3 addresses this issue by adjusting the liquidity frequency distribution by concentrating liquidity around its active trading region (Pa, Pb) as shown in Fig 1. By doing this, the order book within the LP is deepened virtually, thus providing more capital to make larger trades. This is illustrated with the shifting price curve in Fig 2. According to Uniswap, this design enhancement can provide up to 4000x capital efficiency relative to Uniswap V2.
Networking AMMs
In one of our previous articles we chronicled a brief overview of the evolution of AMM protocols. The unifying characteristic that all the aforementioned have is that they are all single AMM protocols. In this section, we are going to be talking about networks of AMMs, or AMM Nets for short. When enshrined into contract code, AMM Nets open a pandoras box of opportunities, as all the previous protocols can be configured into an AMM Net. Liquidity Trees can be considered the simplest class of AMM Nets, and we will be highlighting the advantages of such in this discussion.
If we revisit concentrated liquidity distribution of Fig. 1, the question that we would like to address is how does one employ the capital outside the active trading band so that it is simultaneously earning a return; see Fig 3. We call this inactive region, stagnant liquidity.
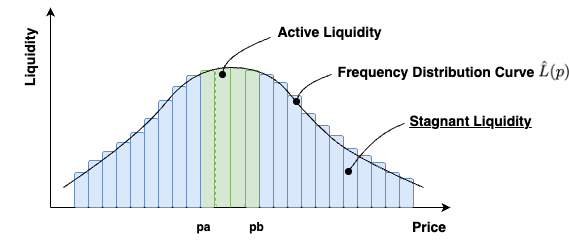
If we reference Fig 3, we address the issue of treating the remaining liquidity outside the active trading band as the stagnant liquidity problem. Unlike addressing this issue using a single LP, as referenced throughout the evolution of the AMM, we address the problem using networks of LPs, called Liquidity Trees.
Simple Tree (Include New Dimension)
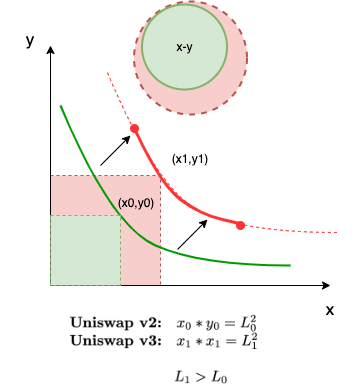
Many degens have proclaimed to us that grasping this concept can be difficult. However, we implore you to not skim over this crucial step, and take the necessary pause and think about what we are doing here. If you can conceptually grasp this part, and (more importantly) why we are doing it, then extending the solution into more general representations is merely step and repeat. So let’s take the common constant product trading (CPT) xy price curve, shown in Fig 2, and extend by including a new dimension as shown in Fig 4.
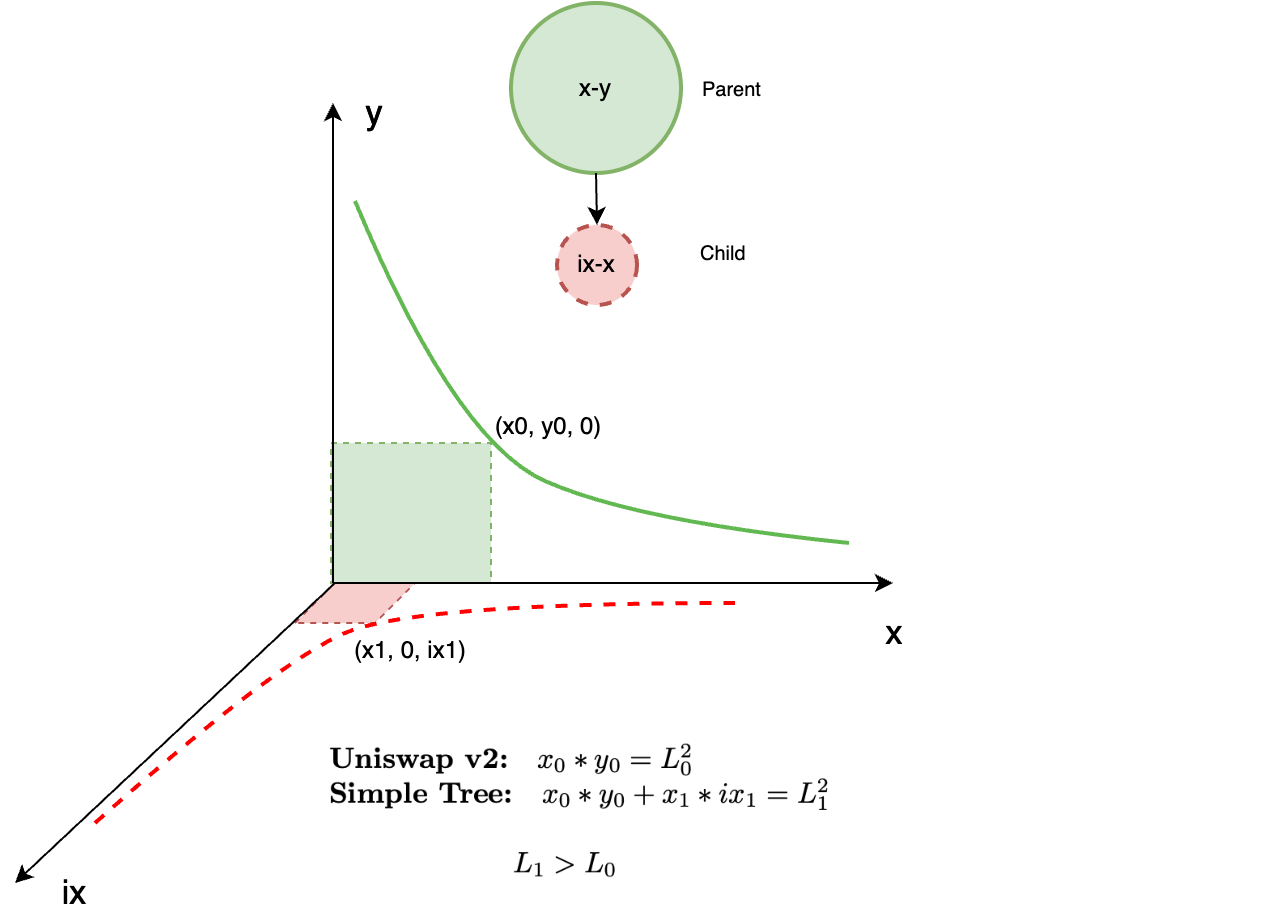
Instead of thinking in terms of x and y, like we would with the standard CPT formula, we are now thinking in terms of x, y and indexed x, otherwise known as ix. When we say indexing, we use the economic definition, which is compiled economic data into a single metric or measurement. In the case of Liquidity Trees, our economic metric is a quantity of LP tokens, measured in terms of either one of the two assets (x or y) as shown in Fig 5. For instance, say we have a USDC/ETH LP and take 10 LP tokens from that pool. We index those 10 LP tokens in terms of USDC or ETH in the form of index tokens defined as iUSDC or iETH. Therefore, as the price of USDC/ETH changes, the quantities of iUSDC or iETH changes as well.
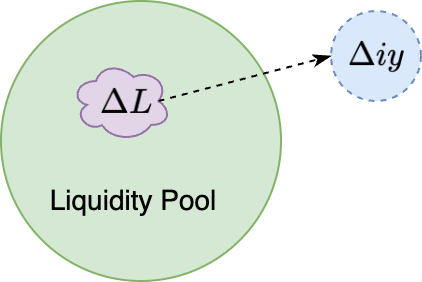
Addressing the CPT indexing problem typically involves solving a linear system of equations, and you can read more about that problem in a previous mediume article of ours titled: The Uniswap Indexing Problem. Without defining and addressing that problem first, we cannot implement a Liquidity Tree.
So let’s recap; to create a Liquidity Tree, we need to take the two LP assets (eg, x and y) and a quantity of LP tokens from its pool and index them into either ix and/or iy. These index tokens are derived from our LP tokens, which are continually rebased into quantities of x and/or y, which are called continual rebased index tokens (CRITs). These CRITs are placed back on the market to form a child LP, and are paired back with one of the original assets x or y from our parent LP; for example see Fig 4.
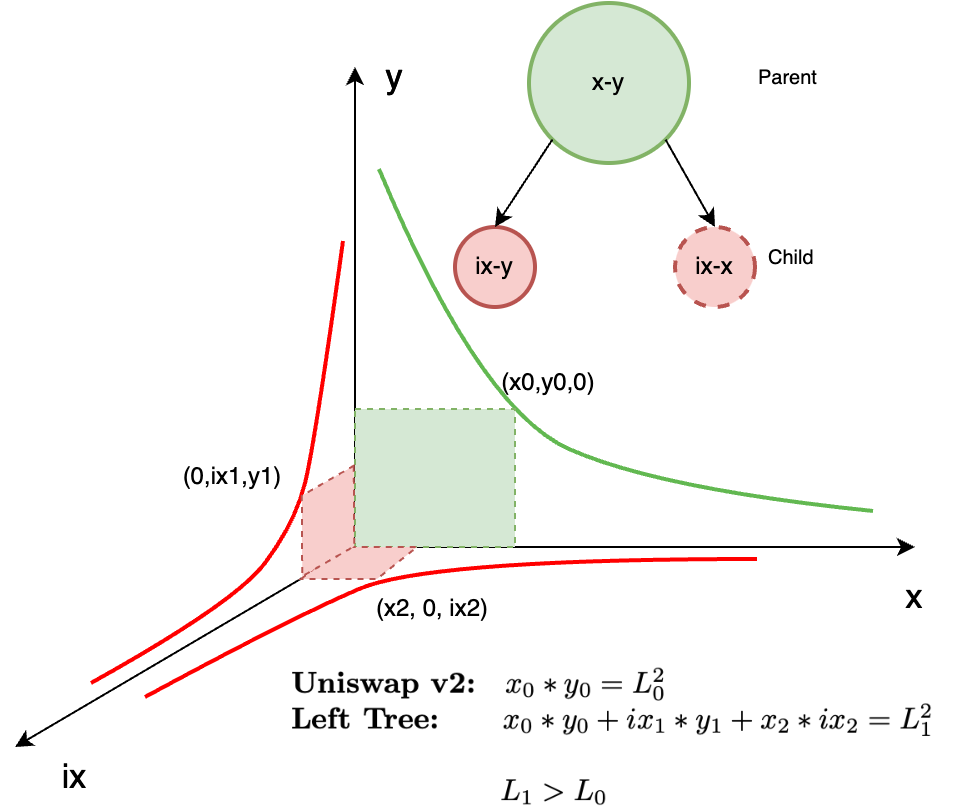
Fig 4 depicts the most rudimentary of Liquidity Trees called a Simple Tree, which consists of one parent and one child LP. If we index x as ix and pair with x, we can represent as curves on the x-y plane for the parent LP and on the ix-x plane for the child LP. Likewise, we can also represent as a computational tree, where nodes represent LP operations and arcs between the nodes represent indexed liquidity transiting from the parent to the child LP.
How Do Liquidity Trees Generate Revenue?
The short answer as to why we include these new dimensions is to earn higher yield from our investment. When we invest into a LP, we receive LP tokens and expect to earn a return from that investment by collecting a share of the trading fees that accrues over time. With a Liquidity Tree, we now have the option of minting index tokens from our invested LP tokens and reinvesting them into the child LP. With this approach, our investment is now making a return both from the parent LP and from the child LP, thus generating higher yield. We are effectively investing into an LP, taking a fully collateralized loan from that investment and reinvesting it. Therefore earning yield from both our original investment and the fully collateralized loan. For the intuition behind this idea, see Fig 6.
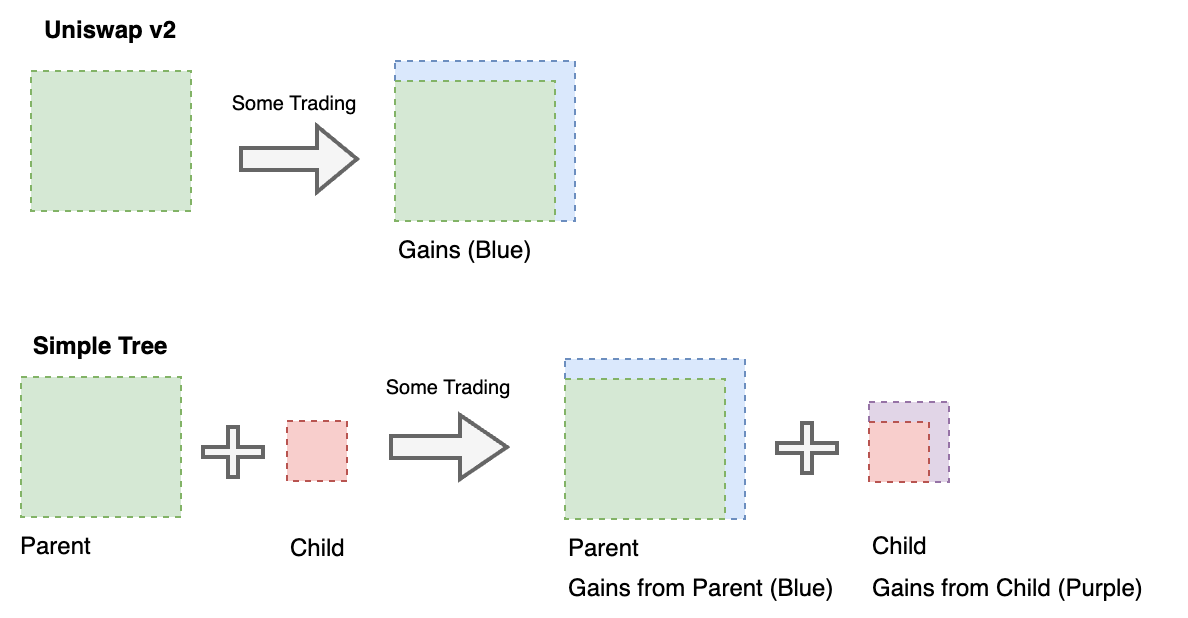
Some of you may be wondering, isn’t the DeFi community doing this with DeFi yield farming? In a round about way, yes but technically no. With classic yield farming, LP token positions are handled manually by end users, and must be continually monitored. However, with Liquidity Trees, we have formalized this process and have enshrined it into contract code by employing CRITs, which can only be made possible by first solving the indexing problem. Hence end users do not need to manually manage the positions, which in turn liberates liquidity providers to do more sophisticated things, and also allows designers to build more sophisticated products. As we will show in later articles, with our soon-to-be released Pachira token, this opens a pandoras box of DeFi products that were not made possible before as decentralized institutional technology. Hence, introducing new emergent effects that have the potential to reshape real-world human sociological behavior.
We can see that by using Liquidity Trees, we have addressed the stagnant liquidity problem, as defined in Fig 3. With this process now formalized, we improve market efficiency. So in short, as we outlined in the evolution of the AMM, instead of addressing this problem using single LPs, we address it using networks of LPs called Liquidity Trees. Since we are the first to formalize this class of AMM Nets, we are not just talking about a single new DeFi primitive, but a new class of DeFi primitives which will define the next epoch of DeFi.
Various Tree Types
If we expand on the Simple Tree idea discussed in the previous section, Liquidity Trees can be represented as computational graphs where nodes denote LP operations and arcs represent indexed capital transitioning between the parent node and the child. Since there are various types of LPs utilized in DeFi (eg, constant weighted product, composable stable, etc.), for the sake of scope, we will only cover the CPT LP.
For a LP of assets x and y, the maximum combinations of child markets that can be formed are ix-y, ix-x, ix-iy, x-iy, and y-iy. A full Liquidity Tree is when all possible asset combinations are utilized, forming the maximum number of child LPs under the parent; refer to Fig. 7 for a visual representation.
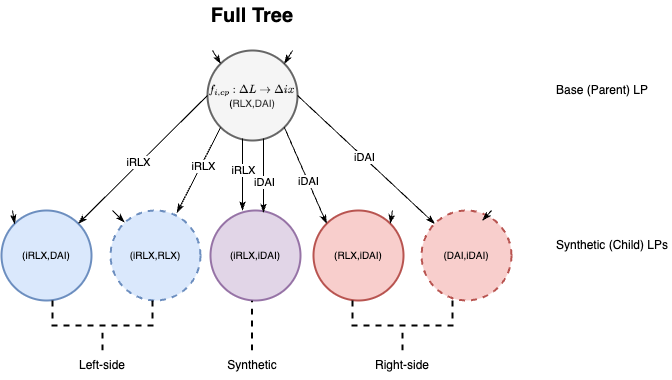
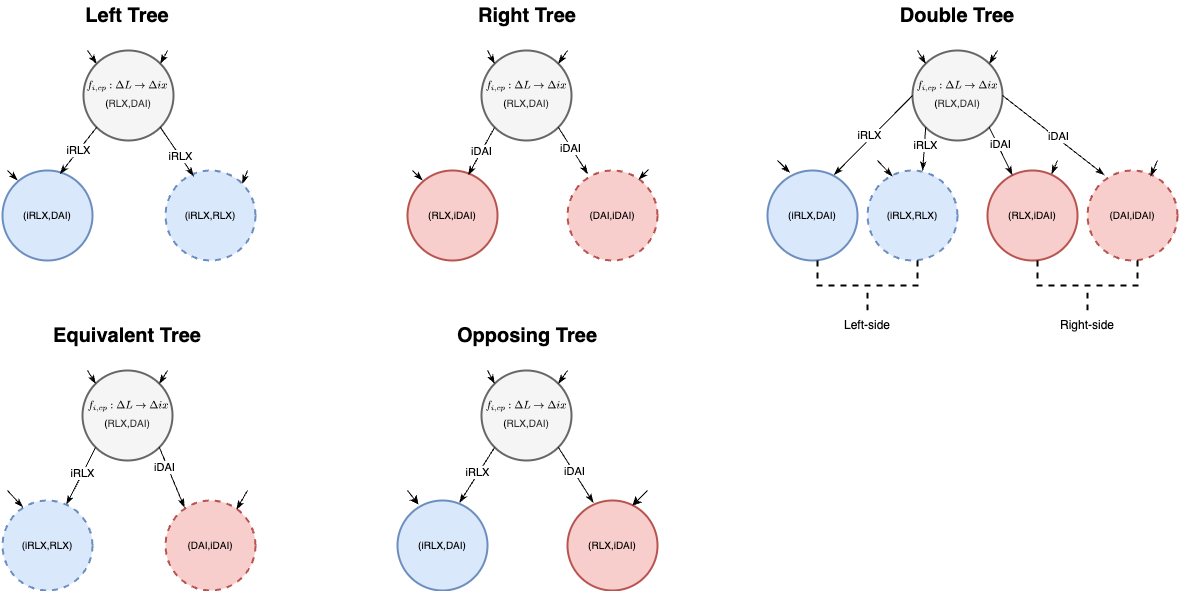
Using other asset combinations, derivations of the full tree from Fig 7 can also be created into various sub-trees; see Fig 8. Simulations have shown us that each of these sub-trees have slightly different nuanced properties which we will discuss in future articles.
Simulation Results
In this section we show simulation output using ETH/USDC price data as our input from Jan 2017-Nov 2023. We ran this on a Uniswap V2 Left-tree setup; see Fig 9.
The swap, deposit and withdraw amounts consist of random non-deterministic samples taken from a Gamma distribution, thus no two simulation runs will produce the same output. To ensure robustness, we ran our simulation through 100 trials and took the medians of the outcomes as displayed in Table 1.
It is important to note that there is an upper bound to the number of minted index tokens that can be deployed into the Liquidity Tree child markets. For instance, if the market cap of our parent pool is $1M USD, then we have access to a maximum of $1M USD that can be minted for index tokens. However in reality, it is highly improbable that a tree’s parent LP will have 100% of its capital deployed into index tokens, as once capital is minted, then it is no longer available for trading. At this stage, we are presuming that it a parent LP will have 10–70% of its capital deployed into index tokens. Which is why we have depicted the red planes of the child LPs in Fig 9 to be considerably smaller than the green plane of the parent LP. Therefore, when we ran these simulations, we conservatively assumed that only 25% of the capital in the parent LP was deployed into the child LPs, as indicated in the first row of Table 1.
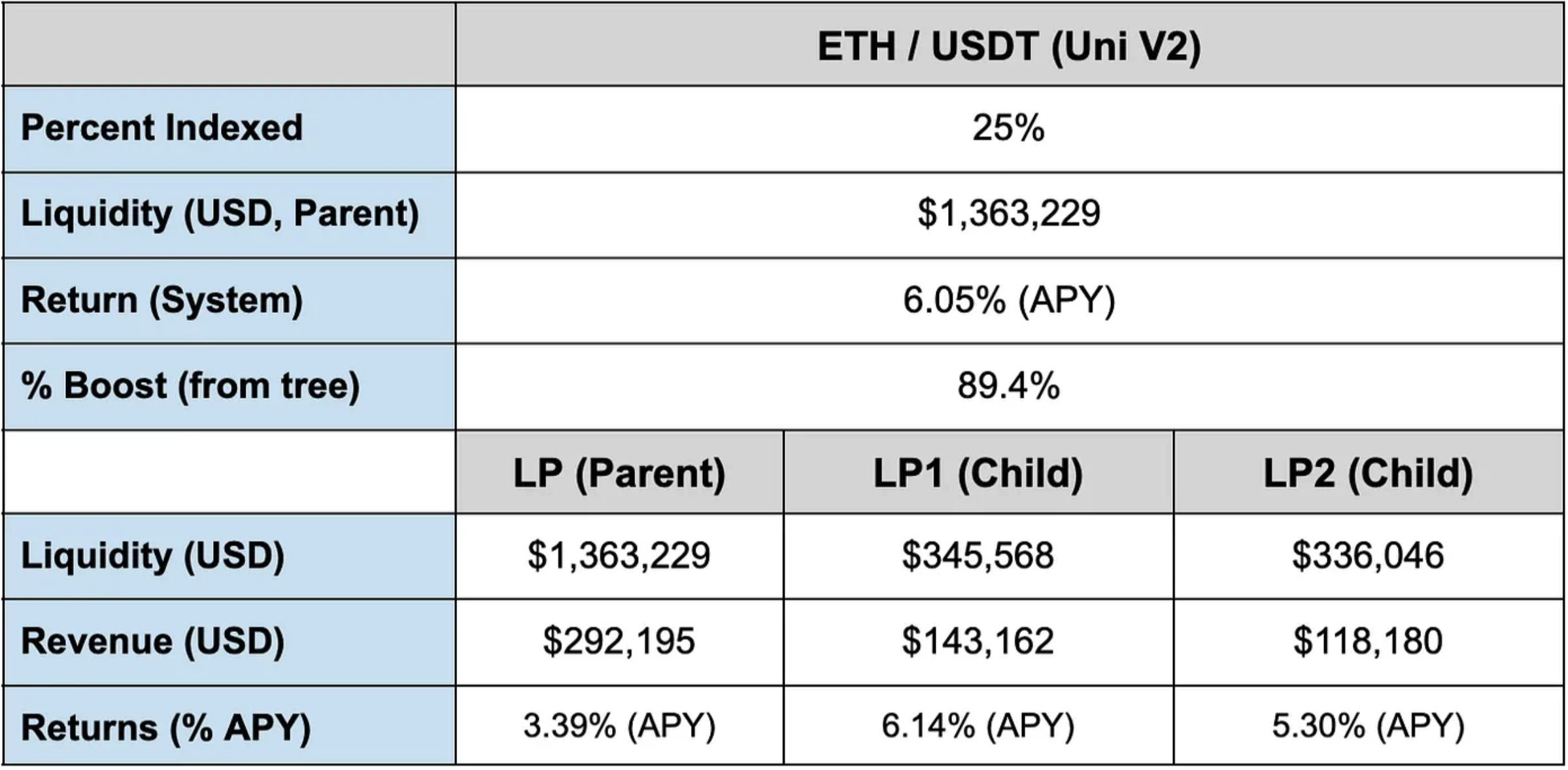
An interesting feature worthy of discussion is that APY within the children is always found to be consistently higher than APY of the parent. We found this to be the case, no matter how many times we ran the simulation, what price samples were used, trade volume, or tree configuration employed. This has to do with how the price of index tokens in the child LPs respond to the price of the native tokens within the parent LP. This is because the volatility of the asset prices in the child LPs is more exacerbated than the volatility of the asset prices in the parent LP. Thus higher volatility in the child assets prices presents arbitrage opportunities that get filled by opportunistic agents (eg. trading bots).
Another interesting feature worth noting is because we see higher volatility in child LP asset prices, it is not necessary to mint a large portion of the capital as index tokens to realize a significant performance boost. This is supported by the simulation outcomes presented in Table 1. Here we see that with only 25% of parent capital deployed as index tokens, an 89.4% performance boost is received from the children. More specifically, our results show we receive a 3.39% annual percentage yield (APY) from the parent, and a system-wide 6.05% APY from the tree as a whole.
If you are interested validating this for yourself and running some Liquidity Tree simulations locally on your machine, please refer to Simulation.